Ondas: Maxwell

las 4 ecuaciones de maxwell:

1-Ley de Gaus.

La ley de Gauss explica la relación entre el flujo del camppo electrónico y una superficie cerrada. Se define como flujo eléctrico ( $\ \Phi$ ) a la cantidad defluido eléctrico que atraviesa una superficie dada. Análogo al flujo de la mecánica de fluidos, este fluido eléctrico no transporta materia, pero ayuda a analizar la cantidad de campo eléctrico ( $\vec{E}$ ) que pasa por una superficie. Matemáticamente se expresa como:

$\Phi = \oint_S \vec{E}_{(r)} \cdot d \vec{S}$

La ley dice que el flujo del campo eléctrico a través de una superficie cerrada es igual al cociente entre la carga (q) o la suma de las cargas que hay en el interior de la superficie y la permitividad eléctrica en el vacío ( $\epsilon_0$ ), así:

$\oint_{S} \vec{E} \cdot d\vec{S} = \frac {q}{\epsilon_0}$

La forma diferencial de la ley de Gauss es

$\vec{\nabla} \cdot \vec{E} = \frac{\rho}{\epsilon_0}$

donde $\rho$ es la densidad de carga en el vacio. Intuitivamente significa que el campo E diverge o sale desde una carga $\frac{\rho}{\epsilon_0}$ , lo que se representa gráficamente como vectores que salen de la fuente que las genera en todas direcciones. Por convención si el valor de la expresión es positivo entonces los vectores salen, si es negativo estos entran a la carga.

Para casos generales se debe introducir una cantidad llamada densidad de flujo eléctrico ( $\vec{D}$ ) y nuestra expresión obtiene la forma:

$\vec{\nabla} \cdot \vec{D} = \rho$

2-Ley de Gauss para el campo magnético:

Experimentalmente se llegó al resultado de que los campos magnéticos, a diferencia de los eléctricos, no comienzan y terminan en cargas diferentes. Esta ley primordialmente indica que las líneas de los campos magnéticos deben ser cerradas. En otras palabras, se dice que sobre una superficie cerrada, sea cual sea ésta, no seremos capaces de encerrar una fuente o sumidero de campo, esto expresa la inexistencia del mono polo magnético. Matemáticamente esto se expresa así:

$\vec{\nabla} \cdot \vec{B} = 0$

donde $\vec{B}$ es la densidad de flujo magnético, también llamada inducción magnética. Es claro que la divergencia sea cero porque no salen ni entran vectores de campo sino que este hace caminos cerrados. El campo no diverge, es decir la divergencia de B es nula.

Su forma integral equivalente:

$\oint_S \vec{B} \cdot d\vec{S} = 0$

Como en la forma integral del campo eléctrico, esta ecuación sólo funciona si la integral está definida en una superficie cerrada.

3-Ley de Faraday-Lenz:

La ley de Faraday nos habla sobre la inducción electromagnética, la que origina una fuerza electromotriz en un campo magnético. Es habitual llamarla ley de Faraday-Lenz en honor a Heinrich Lenz ya que el signo menos proviene de la Ley de Lenz. También se le llama como ley de Faraday-Henry, debido a que Joseph Henry descubrió esta inducción de manera separada a Faraday pero casi simultáneamente. Lo primero que se debe introducir es la fuerza electromotriz ( $\mathcal{E}$ ), si tenemos un campo magnético variable con el tiempo, una fuerza electromotriz es inducida en cualquier circuito eléctrico; y esta fuerza es igual a menos la derivada temporal del flujo magnético, así:

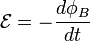$\mathcal{E} = - \frac{d \phi_B}{d t}$ ,

como el campo magnético es dependiente de la posición tenemos que el flujo magnético es igual a:

$\phi_B = \int_{S} \vec{B} \cdot d\vec{S}$ .

Además, el que exista fuerza electromotriz indica que existe un campo eléctrico que se representa como:

$\mathcal{E} = \oint \vec{E} \cdot d\vec{l}$

con lo que finalmente se obtiene la expresión de la ley de Faraday:

$\oint \vec{E} \cdot d\vec{l} = - \ { d \over dt } \int_{S} \vec{B} \cdot d\vec{S}$

Lo que indica que un campo magnético que depende del tiempo implica la existencia de un campo eléctrico, del que su circulación por un camino arbitrario cerrado es igual a menos la derivada temporal del flujo magnético en cualquier superficie limitada por el camino cerrado.

El signo negativo explica que el sentido de la corriente inducida es tal que su flujo se opone a la causa que lo produce, compensando así la variación de flujo magnético (Ley de Lenz).

La forma diferencial de esta ecuación es:

$\vec{\nabla} \times \vec{E} = - \frac{\partial \vec{B}}{\partial t}$

Se interpreta como sigue: si existe una variación de campo magnético B entonces este provoca un campo eléctrico E. En presencia de cargas libres como los electrones el campo E puede desplazar las cargas y producir una corriente eléctrica. Esta ecuación relaciona los campos eléctrico y magnético, y tiene otras aplicaciones prácticas cómo los motores eléctricos y los generadores eléctricosy explica su funcionamiento. Más precisamente, demuestra que un voltaje puede ser generado variando el flujo magnético que atraviesa una superficie dada.

4-Ley de Ampère generalizada:

Ampère formuló una relación para un campo magnético inmóvil y una corriente eléctrica que no varía en el tiempo. La ley de Ampère nos dice que la circulación en un campo magnético ( $\vec{B}$ ) a lo largo de una curva cerrada C es igual a la densidad de corriente ( $\vec{J}$ ) sobre la superficie encerrada en la curva C, matemáticamente así:

$\oint_C \vec{B} \cdot d\vec{l} = \mu_0 \int_S \vec{J} \cdot d\vec{S}$

donde $\ \mu_0$ es la permeabilidad magnética en el vacío.

Pero cuando esta relación se la considera con campos que sí varían a través del tiempo llega a cálculos erróneos, como el de violar la conservación de la carga. Maxwell corrigió esta ecuación para lograr adaptarla a campos no estacionarios y posteriormente pudo ser comprobada experimentalmente. Maxwell reformuló esta ley así:

$\oint_C \vec{B} \cdot d\vec{l} = \mu_0 \int_S \vec{J} \cdot d\vec{S} + \mu_0 \epsilon_0 \frac{d}{dt} \int_S \vec{E} \cdot d\vec{S}$

En el caso específico estacionario esta relación corresponde a la ley de Ampère, además confirma que un campo eléctrico que varía con el tiempo produce un campo magnético y además es consecuente con el principio de conservación de la carga.

En forma diferencial, esta ecuación toma la forma:

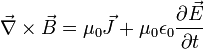
$\vec{\nabla} \times \vec{B} = \mu_0 \vec{J} + \mu_0 \epsilon_0 \frac{\partial \vec{E}}{\partial t}$

Las ecuaciones de Maxwell como ahora las conocemos son las cuatro vistas anteriormente y que resumidamente se pueden encontrar en la siguiente tabla:

Nombre	Forma diferencial	Forma integral
Ley de Gauss:	$\vec{\nabla} \cdot \vec{E} = \frac{\rho}{\epsilon_0}$	$\oint_{S} \vec{E} \cdot d\vec{s} = \frac {q}{\epsilon_0}$
Ley de Gauss para el campo magnético:	$\vec{\nabla} \cdot \vec{B} = 0$	$\oint_S \vec{B} \cdot d\vec{s} = 0$
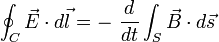
Ley de Faraday:	$\vec{\nabla} \times \vec{E} = - \frac{\partial \vec{B}}{\partial t}$	$\oint_C \vec{E} \cdot d\vec{l} = - \ { d \over dt } \int_{S} \vec{B} \cdot d\vec{s}$
Ley de Ampère generalizada:	$\vec{\nabla} \times \vec{B} = \mu_0 \vec{J} + \mu_0 \epsilon_0 \frac{\partial \vec{E}}{\partial t}$

Ondas

lunes, 19 de marzo de 2012

Maxwell

4-Ley de Ampère generalizada: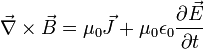

No hay comentarios:

Publicar un comentario